En el1545 Girolamo Cardano publica Ars Magna, en el que presenta la solución general de la ecuación cúbica y la de la cuártica. Dicha publicación causó tal impacto en el mundo del álgebra que generalmente se considera el año 1545 como el que marca el período moderno en matemáticas. Pero, ¿fue Cardano el verdadero descubridor de los métodos de resolución de dichos tipos de ecuaciones?
A mediados del siglo XVI, Niccolo Fontana, llamado Tartaglia por su condición de tartamudo, se trasladó a Venecia. Tartaglia llegó a ser famoso en la zona por sus trabajos realizados para los ingenieros del Arsenal veneciano.
Estando en la ciudad de los canales llegó a sus oídos que un tal Antonio Maria del Fiore presumía de conocer la fórmula maravillosa para resolver la ecuación cúbica. Dicha fórmula, según del Fiore, le había sido entregado por parte de un gran matemático 30 años antes. El hecho de que existiera alguna posibilidad de resolver la cúbica llevó a Tartaglia a trabajar en el desarrollo de un método de resolución, consiguiéndolo algo después.
Cada uno de ellos propuso 30 cuestiones al otro contendiente que tenían que ser resueltas en un tiempo concreto. Los de Tartaglia trataban sobre temas aritméticos, geométricos y algebraicos. Lo de del Fiore tenían todos la misma temática: ecuaciones cúbicas sin término de grado dos. Cuando llegó el día fijado para la presentación de las soluciones, Tartaglia había resuelto todos los problemas propuestos por del Fiore, pero éste no había podido dar respuesta a ninguna de las cuestiones propuestas por Tartaglia. Ni siquiera uno en el que se debía resolver una ecuación cúbica, para la que Tartaglia conocía un método particular.
Pero había un pequeño problema: en ciertas ecuaciones que parecían normales aparecían soluciones en las que se podía encontrar una raíz cuadrada con radicando negativo (estas ecuaciones son las que más adelante se llamarían irreducibles). Teniendo en cuenta que, como hemos comentado antes, en esta época ni siquiera los números negativos estaban demasiado aceptados, la aparición de este tipo de soluciones se veía como algo bastante extraño.
Scipione del Ferro. Él fue realmente quien encontró la fórmula de la resolución de la cúbica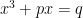 
(Tartaglia también encontró métodos de resolución, pero se cree que dichos métodos no fueron descubiertos totalmente por él, sino que la idea provenía de alguna fuente anterior;
Formula
(Tartaglia también encontró métodos de resolución, pero se cree que dichos métodos no fueron descubiertos totalmente por él, sino que la idea provenía de alguna fuente anterior;Formula
